
4 Ways to Add, Augment, or Excite Upper Harmonics
Adding upper harmonics is a great way to make a sound more exciting and present in the mix. In this article, we’ll discuss several ways to add upper harmonics.
It’s common to come across dull elements in a mix. The instrument may be correct, the part it plays may be correct, but it still doesn’t sound exciting. By adding upper harmonics, we can introduce a fuller, grittier, brighter character to a sound—depending on the original signal, of course. These additional frequencies can create interesting timbres that your audience can enjoy listen after listen.
In this article, we’ll cover four processes that can be used to add or augment upper harmonics in order to liven a dull mix element. This will include distortion, saturation, compression, and harmonic excitation.
Understanding harmonics
To understand why some of these processors introduce new frequency information to an existing audio signal, we should first quickly cover the concept of harmonics.
Anatomically, sound is a wave oscillating at a certain frequency. This base frequency is called the fundamental frequency and mathematically determines any additional frequencies that can be found in an audio signal.
Sine wave
The simplest wave is the sine wave, a continuous and smooth curve oscillating between a positive and negative value.
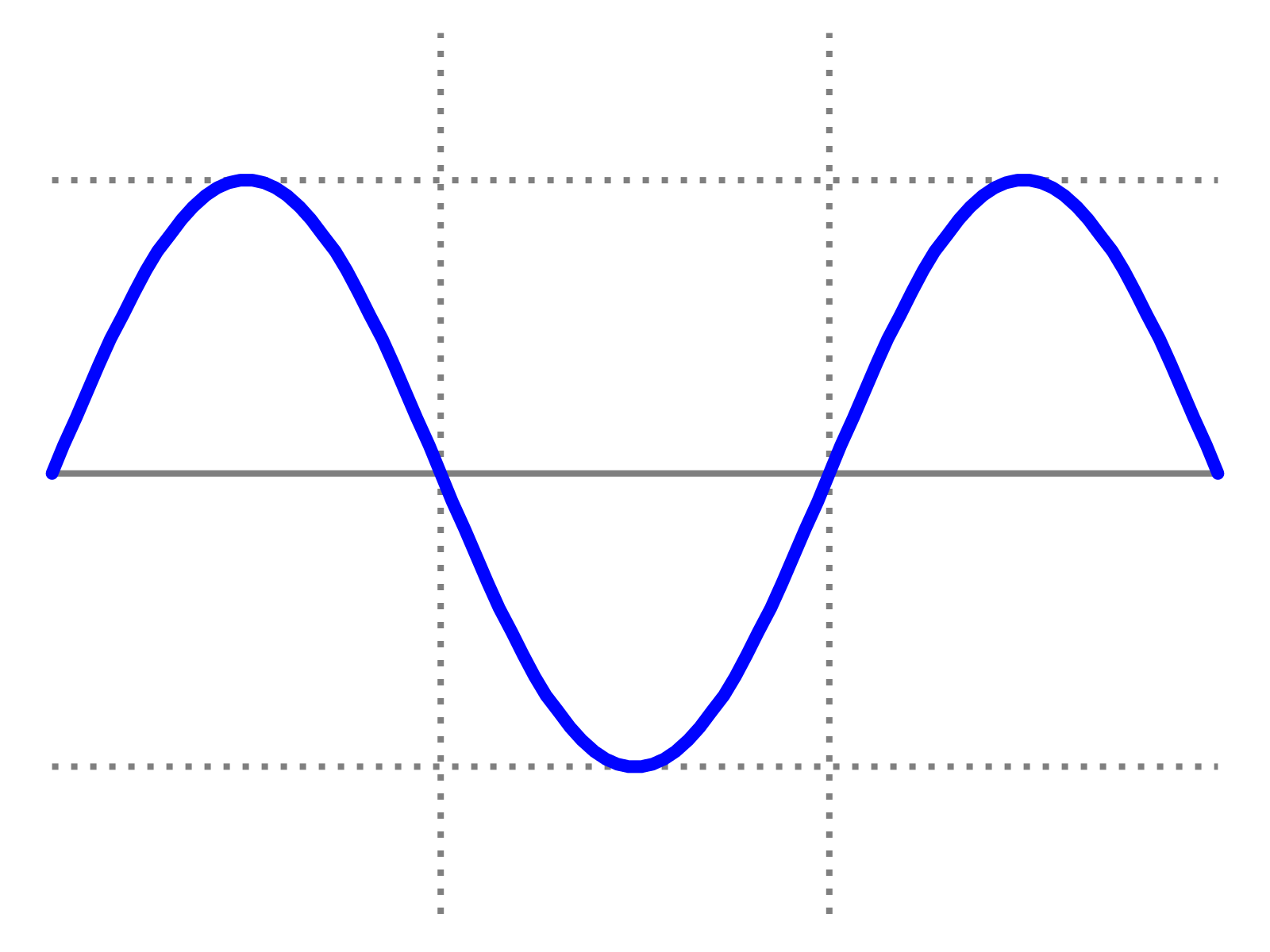
Sine wave
A sine wave is easy to pick out with its characteristically rounded timbre. This is due to its quite simple frequency content. Notice in the spectral analyzer below that the sine wave has a single spike at 198 Hz.

Sine wave frequency content
For clarification, the high-frequency content that you see in the spectral analyzer is the latent noise in my audio system, or the noise floor. Notice that it’s all below -114 dB, effectively inaudible compared to the sine wave.
More complex waveshapes—any shape other than a sine wave—will contain additional tones at other frequencies, which are harmonically related to the fundamental frequency.
These additional tones are called harmonics, the total collection of which are located at whole number multiples of the fundamental frequency. Therefore, a tone at 100 Hz could have harmonics at 100 Hz, 200 Hz, 300 Hz, 400 Hz, etc.
The sine wave has one harmonic, the first harmonic, which is located at the frequency expressed as fundamental frequency x 1. This is obviously still the same pitch as the fundamental frequency, meaning the sine wave’s frequency content is composed only of the fundamental frequency.
Three of the most commonly known complex waves are the sawtooth, square, and triangle waves. These waves differ in whether they include harmonics located at even-number multiples of the fundamental frequency—“even harmonics”—those located at odd-number multiples—“odd harmonics”—or both. The amplitude of these harmonics may also differ.
As a general rule, we tend to find even harmonics to be less jarring and more pleasant than odd harmonics.
Sawtooth wave
The sawtooth wave contains all harmonics, both those located at even and odd multiples of the fundamental. With the inclusion of all harmonics, the sawtooth wave’s timbre is bright and harsh.

Sawtooth wave

Sawtooth wave frequency content
Square wave
The square wave contains all odd harmonics. While generally not as bright as the sawtooth, the square wave still has quite a harsh timbre.

Square wave

Square wave frequency content
Triangle wave
The triangle wave, like the square wave, includes all odd harmonics. Harmonics generally have lower amplitudes than the fundamental frequency and decrease in amplitude as we go up the audible frequency spectrum. However, the amplitudes of harmonics in a triangle wave decrease much quicker than a square wave’s do. Because of this, the triangle wave is harsher than a sine wave, but not as bright as a square wave.

Triangle wave

Triangle wave frequency content
Notice that there is effectively no difference between one of the upper harmonics in a complex wave—like a sawtooth, square, or triangle wave—and a sine wave at the frequency and amplitude of that harmonic.
According to the findings of 18th century mathematician Joseph Fourier, we can effectively recreate the harmonic content of a complex wave using a series of sine waves positioned at the proper frequencies. These waves, when summed as one audio signal, will sound like the complex wave.
Using the same logic, if we can somehow make an audio signal such as a sine wave more like a square wave, we can introduce additional harmonics to a previously simple signal. This is more or less the way that the following processors create and augment mathematically related upper harmonics from an input signal that doesn’t contain these frequencies in the first place.
Distortion
Distortion has been used to add upper harmonics for decades. Think about the sonic differences between a distorted electric guitar and its clean, undistorted counterpart. The distorted guitar seems to have richer harmonic content, filling the frequency spectrum more densely than a clean signal.
Whether in an analog or digital context, distortion is the result of a signal’s amplitude exceeding the limits of the audio system. The system doesn’t have a way to accurately record these peaks, only recognizing that the signal was approaching the limit and is somewhere above it.
Because the system can’t accurately recreate a signal that passes its limit, the system sets the signal’s amplitude at the highest possible value: the limit itself. As a result, the signal’s waveform at these peaks is essentially cut off.
We call this hard clipping, where signal is unaffected until it reaches the limit, when peaks are then completely flattened until signal falls into a recreatable amplitude again.

Hard clipping
Notice that as the sine wave’s peaks are flattened, it becomes more and more similar to a square wave. As we mentioned before, the square wave contains odd harmonics, and therefore has a harsh and brittle tone.
This “squarification” of the audio signal produces upper harmonics that are harmonically related to the original audio signal’s frequency.
Hard clipping can have an aggressive sound, completely destroying the integrity of an audio signal if pushed to the extremes. By over-introducing upper harmonics, the frequency content of the original signal becomes less intelligible, causing the output to represent the original signal less and less.
At these extreme levels, distortion is great for adding grit and creating an aggressive tone. In the audio examples below, I’ve demonstrated this drive on a bass, electric piano, and vocal using


Trash 2
Here are the dry sounds:
Now, here are the same sounds with heavy distortion:

Heavily distorted bass

Heavily distorted electric piano

Heavily distorted vocal
At more moderate levels, or in the case of tube distortion—which creates even harmonics—distortion can have a “warming” effect, subtly adding upper harmonics to create a more dense sound. Below, I’ve demonstrated lighter distortion using the same sounds:
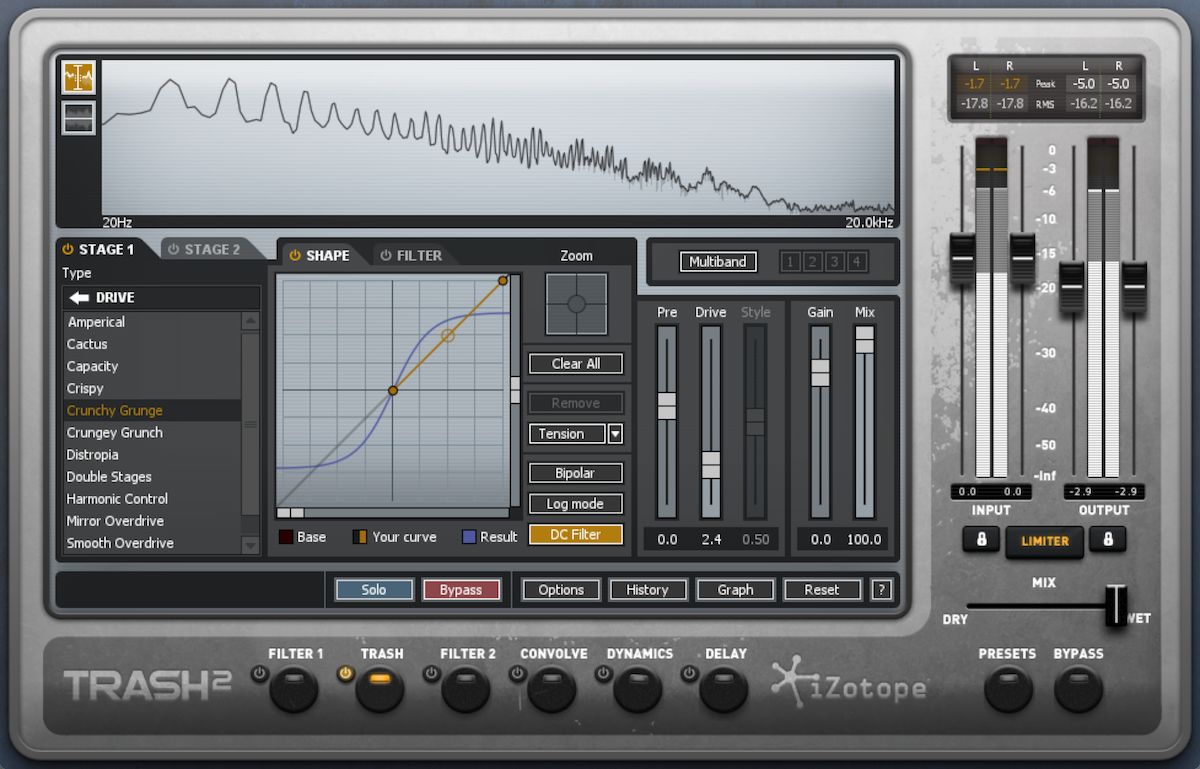
Lightly distorted bass
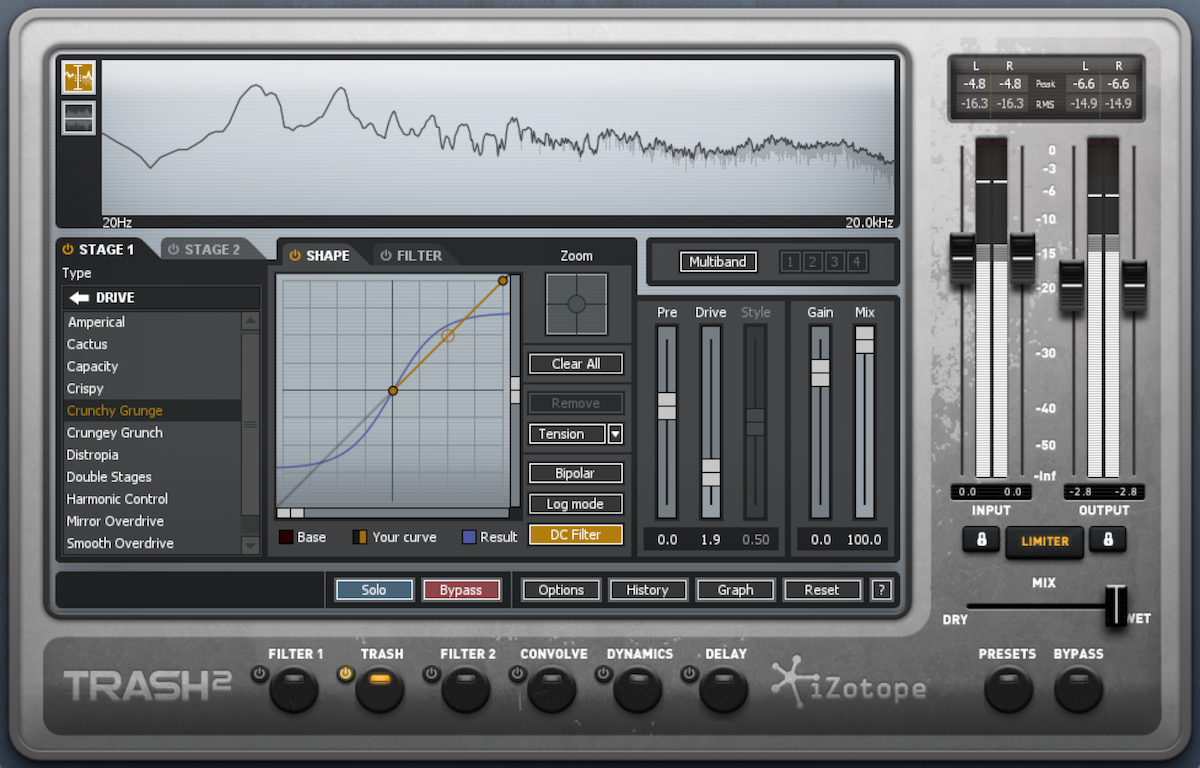
Lightly distorted electric piano
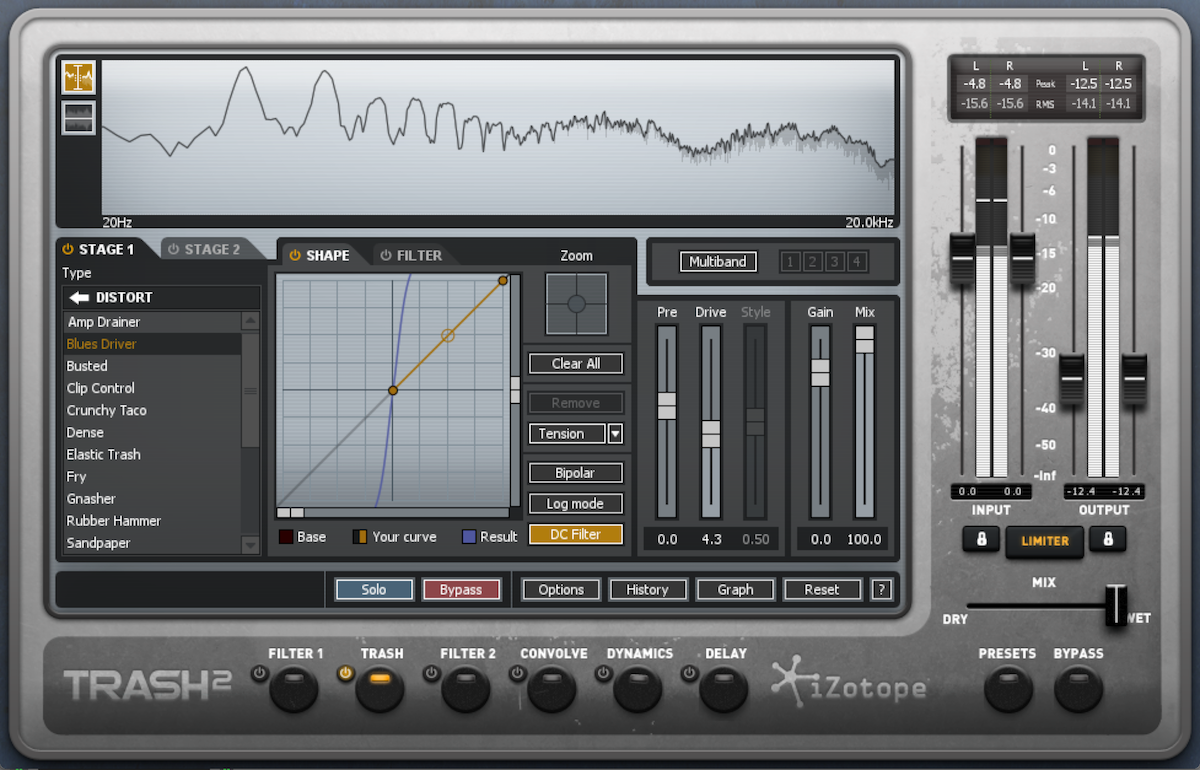
Lightly distorted vocal
Saturation
Saturation is very similar to distortion in both its cause and sonic character. However, there’s enough of a distinction that it’s worth noting the difference.
The common saturation effect in modern digital audio production references the effect of tape saturation in analog recording contexts. Again, as in the case of distortion, saturation is caused when a signal’s amplitude exceeds the limits at which it can be recorded and recreated.
However, magnetic tape used in analog recording does not react like a circuit or a digital audio system. Instead, due to the chemical composition of magnetic tape, a lighter, compression-like effect occurs.
We call this soft clipping, as the peaks of an audio signal are more gently rounded when approaching the system limit, rather than being completely chopped off like in hard clipping.

Soft clipping
As a result, saturation is generally quite a pleasant effect. It can add the warmth of gentle distortion and can often be pushed harder than distortion without the audio signal completely breaking down.
As saturation doesn’t introduce the harshness of distortion, it’s great for adding upper harmonics to “fatten” low-frequency sounds, as well as for gluing groups of elements together.
I’ve run the previous three sounds through some saturation using Trash 2’s “Tape Saturation” distortion type to demonstrate the sonic differences between saturation and distortion:

Lightly distorted vocal

Lightly distorted vocal
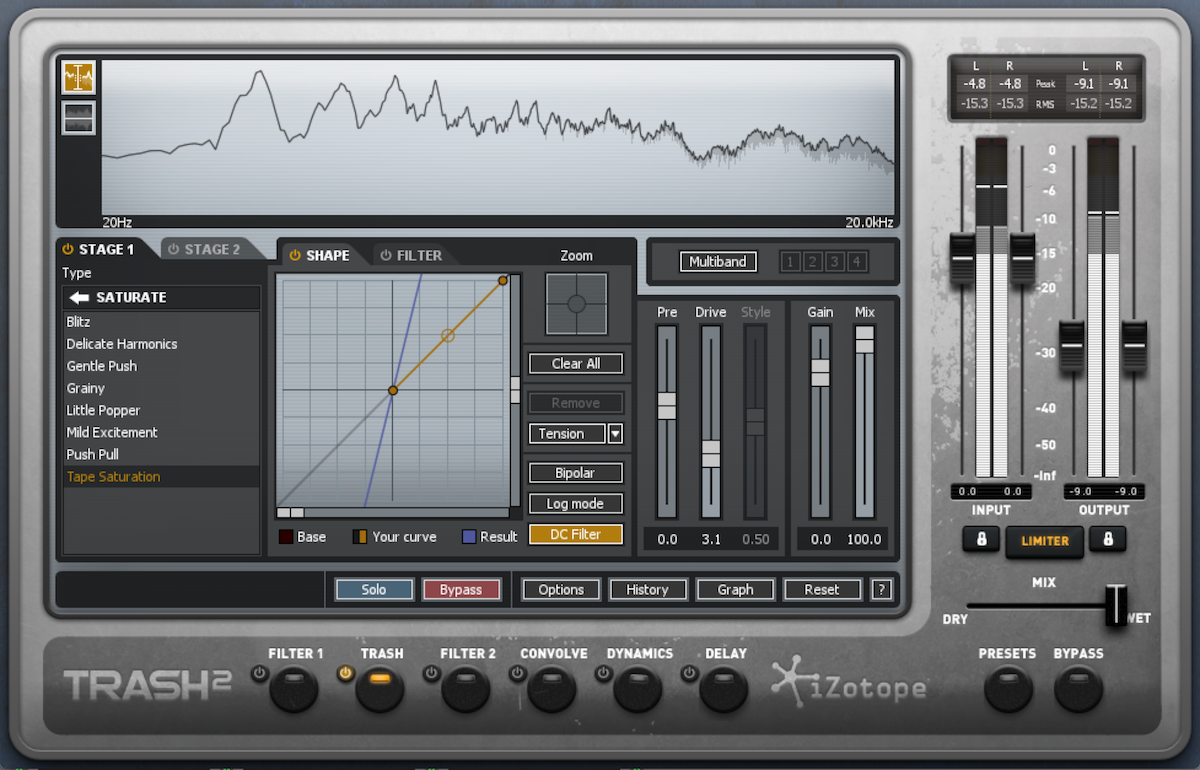
Lightly distorted vocal
Hard compression
You should notice that distortion and saturation both function by compressing the peaks of an audio signal when its amplitude passes a certain threshold. This process should sound pretty familiar, as it’s the basis for common compression.
Therefore, as distortion and saturation can create and augment upper harmonics, standard compression can cause a similar effect.
The main distinction between compression and distortion/saturation is that compression generally acts much more slowly, as distortion and saturation effectively have no attack time. Therefore, moderate compression usually does not result in the clipping caused by the two previous processors.
Hard compression, however, with a fast enough attack time and a high enough ratio—like in the case of a limiter—can begin to emulate the effects of clipping. Therefore, we can use hard compression or hard parallel compression to achieve similar results to distortion or saturation.
Generally, distortion is a more specialized way to introduce an aggressive sound than hard compression is. We can use hard parallel compression, however, to achieve a more driven sound while maintaining the ability to balance the hard-compressed signal with the unprocessed signal.
Again, I’ve processed the previous three sounds with some hard parallel compression:
Parallel processing can be used to implement any of the effects that we’re discussing today. Head here for a more detailed discussion on parallel compression, distortion, and saturation.
Harmonic excitation
Harmonic exciters are quite similar to distortion and saturation, in that they add upper harmonics through the process of distortion. The main difference is that they tend to introduce upper harmonics only in a certain range of the frequency spectrum.
The Aphex Aural Exciter, introduced in the 1970s, functioned essentially by performing parallel distortion to a high-passed version of the original signal.

Aphex Aural Exciter
By exclusively distorting this frequency band and mixing this new signal with the original, harmonic excitation provides a harmonically-related crispness that isn’t replicable with standard EQ methods.
Therefore, harmonic exciters are great for processing vocals to increase presence and intelligibility, as well as the master bus to add some air to a mix. Due to the fact that an exciter can easily brighten a sound, it’s best to use the effect in moderation.
Modern excitation plug-ins, like the exciters found in


Neutron 5


Ozone 12 Advanced
In the following audio examples, I’ve processed our bass, electric piano, and vocal using the Exciter found in Ozone 9. To simulate the effect of an old exciter, I’ve done this lightly in the high frequencies.

Bass - Excited
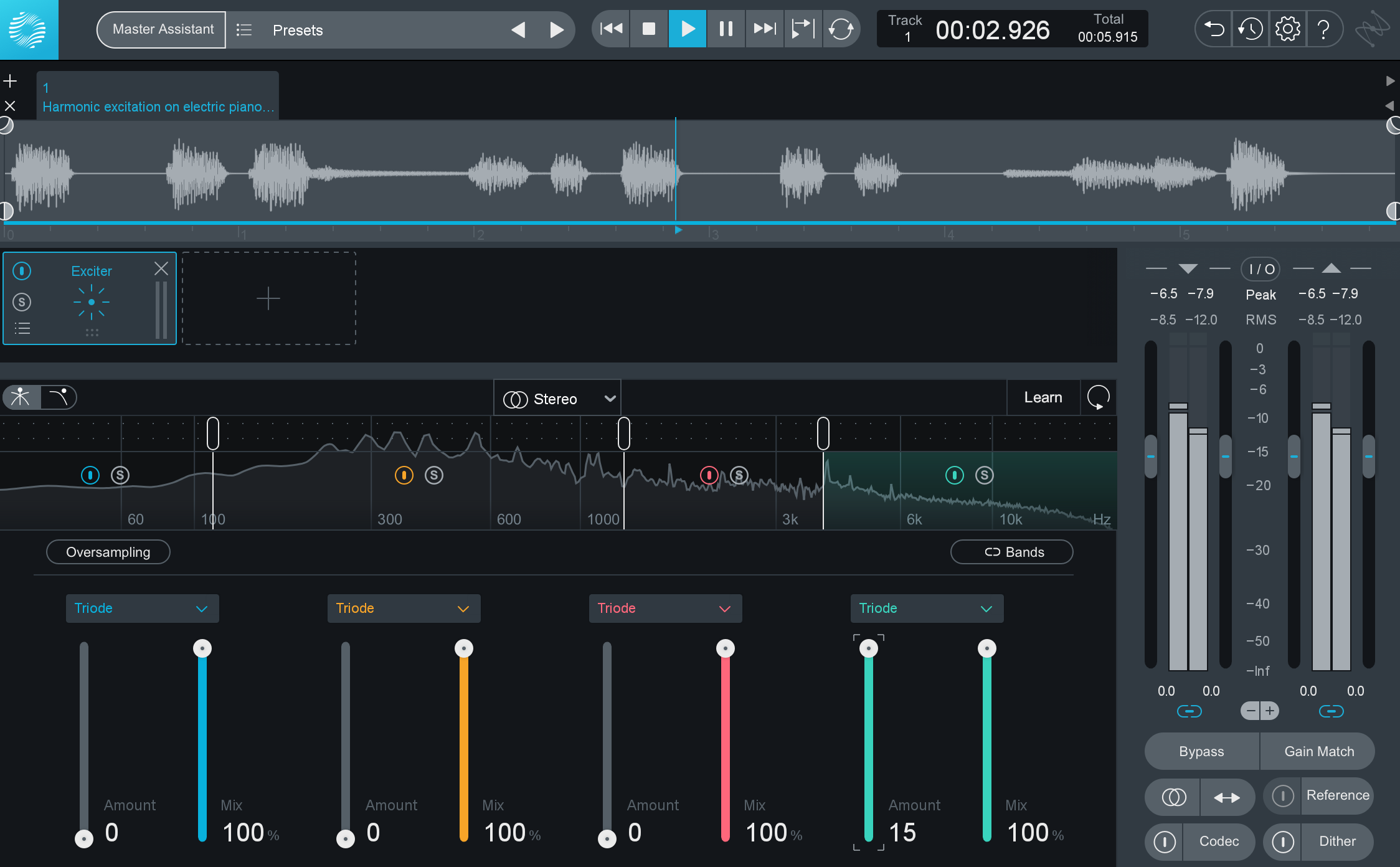
Electric Piano - Excited
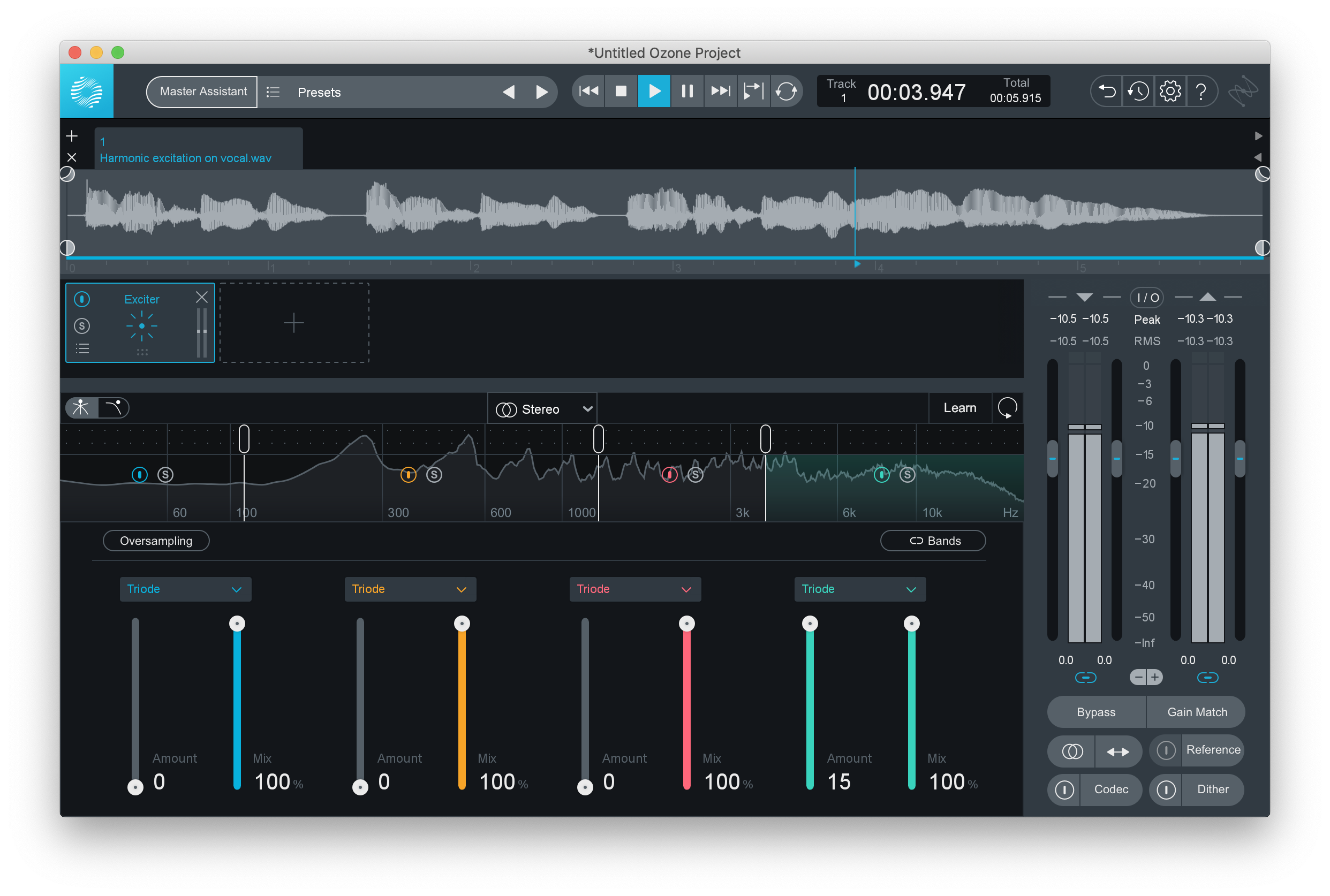
Vocal - Excited
Conclusion
Through these methods, individual elements, groups of elements, or even the entire mix can be injected with some life with the introduction of upper harmonics. This can lead to a fuller, warmer, or harsher sound depending on how hard you push the effect processors.
By cranking up a distortion, saturation, compression, or harmonic excitation unit, we can create aggressive and characteristic sounds that give a track plenty of energy.
And with a more subtle approach, we can make an element sound more impactful to a listener without it becoming overbearing, livening up the listener’s experience and making a track more pleasing to the ear.
